5.4 Funciones (Inyectiva, Suprayectiva, Biyectiva).

Esta clasificación obedece a la forma en que están relacionados los elementos del dominio con los del recorrido. Conviene utilizar la notación: f | Df → Cf “función que mapea al dominio Df en el recorrido Cf”.

Función inyectiva (uno a uno): es inyectiva o uno a uno y se denota como 1-1, si a diferentes elementos del dominio le corresponden diferentes elementos del codominio. En esta función, para dos valores cualesquiera x1 y x2 de su dominio se cumple que: x1 es diferente de x2, entonces f(x1) es diferente que f(x2).

Ejemplo: La función f(x) = 3x + 1 es 1-1 ya que si se define como f | R → R entonces se tendrá que a diferentes elementos del dominio les corresponden diferentes elementos del codominio.

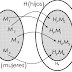
Ejemplo: Sea M el conjunto de mujeres con hijos, H el conjunto de los hijos y f la función que asocia a cada mujer con su hijo primogénito. Es una función 1-1 o inyectiva.

Para comprobar gráficamente que una función es 1-1 basta con comprobar que toda recta paralela al eje "x" corta a la gráfica de la función en un solo punto a la vez.

Función suprayectiva (sobre): Una función es suprayectiva o sobre si todo elemento de su Codominio es imagen de por lo menos un elemento de su Dominio.

Si para toda b ∈ Cf, existe a ∈ Df tal que f(a) = b, entonces f es sobreyectiva.

Otra forma de expresar que una función es sobre es decir que debe cumplir con que su Codominio y su Recorrido sean iguales.

Ejemplo: Sea la función f(x) = 3x + 1 definida como f | R → R. En este caso se ve que todo número real es imagen de algún otro número real bajo la función f. Esto significa que el recorrido es igual al codominio y por lo tanto la función dada es suprayectiva o sobre.

Función biyectiva (1-1 y sobre): Una función es biyectiva si al mismo tiempo es inyectiva y suprayectiva, y la relación entre los elementos del dominio y los del codominio es biunívoca.

 Una función puede ser:

I) 1-1 y sobre (biyectiva). 

II) 1-1, pero no sobre. 

III) No 1-1, pero sí sobre. 

IV) Ni 1-1 ni sobre.