6.4 Arboles.
6.4 Arboles
Cuando se aprende o se enseña un nuevo concepto en el ámbito de las matemáticas, considero que ayuda mucho saber en donde se puede aplicar dicho concepto, por ejemplo, cuando aprendí el Teorema de Pitágoras, el cuadrado de la hipotenusa es igual a la suma del cuadrado de los catetos, se me grabó más cuando supe que lo podía usar para determinar la altura de un árbol o el ancho de un río.
De igual forma sucede con el concepto de árboles en Matemática Discreta, considero que si sabemos cuál es su aplicación vamos a entenderlo mejor.
Todos en algún momento nos hemos visto en la necesidad de buscar un archivo en algún lugar de nuestra computadora ya sea porque no nos acordamos de la ubicación o simplemente porque queremos saber si está guardado allí; sin saberlo, hasta ahora, la forma en que el sistema operativo lo busca es usando la teoría de árboles, en este caso, árboles binarios.
Los hemos usado en gramática (árboles gramaticales), en adminsitración (árboles jerárquicos), en biología (árboles genealógicos), en cada libro o página web que leemos (árboles de contenido) y principalmente en los motores de búsquedas en internet (árboles binarios).
Todos en algún momento nos hemos visto en la necesidad de buscar un archivo en algún lugar de nuestra computadora ya sea porque no nos acordamos de la ubicación o simplemente porque queremos saber si está guardado allí; sin saberlo, hasta ahora, la forma en que el sistema operativo lo busca es usando la teoría de árboles, en este caso, árboles binarios.
Los hemos usado en gramática (árboles gramaticales), en adminsitración (árboles jerárquicos), en biología (árboles genealógicos), en cada libro o página web que leemos (árboles de contenido) y principalmente en los motores de búsquedas en internet (árboles binarios).
 |
| Árbol de contenidos - Libros, páginas Web |
 |
| Árbol genealógico - Biología |
 |
| Árbol Jerarquico - Administración |
 | |||
| Árbol gramatical |
 |
| Motores de búsqueda |
| En Estructura de Datos, se usan para organizar y relacionar datos de una base de datos. |
 |
| Bases de datos |
Definiciones:
- Desde el punto de vista conceptual, un árbol es un caso particular de grafo, es un objeto que comienza con una raíz y se extiende en ramificaciones o lineas que terminan en un nodo.
- Representan la estructura no-lineal y dinámica de datos más importante en computación. Dinámica porque puede cambiar durante la ejecución de un programa y no-lineal porque a cada elemento del árbol pueden seguirle varios elementos.
- Es un conjunto de nodos y líneas. Un nodo es un elemento de información que reside en un árbol. Una línea es un par de nodos ordenados, <u,v>, y a la secuencia de lineas se le llama ruta (path).
Propiedades:
- Tiene un nodo al que se le llama "nodo raíz" o raíz del árbol, éste no tiene "padre".
- Todos los nodos tienen una sola línea de entrada, excepto el nodo raíz, éste no tiene línea de entrada.
- Existe una "única" ruta del nodo raíz a todos los demás nodos del árbol.
- Si existe una ruta <a,b>, entonces "b" es el "hijo" de "a" y es el nodo raíz de un sub-árbol.
- Todos los nodos que son descendientes de un mismo nodo "padre", son "hermanos".
- Todo nodo que no tiene ramificaciones (hijos), es un nodo "terminal" u "hoja".
- Todo nodo que no es raíz ni terminal es un nodo "interior".
- "Grado" es el número de descendientes directos de un determinado nodo.
- "Grado del árbol" es el máximo grado de todos los nodos del árbol.
- "Nivel" es el número de ramificaciones que se deben recorrer para llegar a un determinado nodo. El nodo raíz tiene nivel 1.
- "Altura del árbol" es el máximo número de niveles de todos los nodos del árbol.
Representación:

Longitud de un árbol:
Es el número de arcos que deben ser recorridos desde la raíz hasta el nodo X.Longitud de camino interno:
Es la suma de las longitudes de camino de todos los nodos del árbol.en donde i = nivel del árbol, h = altura del árbol, ni = número de nodos en el nivel "i".
Media de la longitud de camino interno:
Es el número de arcos que deben ser recorridos en promedio para llegar de la raíz a un nodo cualquiera del árbol.en donde LCI = longitud de camino interno y "n" =número de nodos del árbol.
Longitud de camino externo:
Árbol extendido: es aquel en el que el número de hijos de cada nodo es igual al grado del árbol.
Para que se cumpla esta condición si es necesario se le agregan nodos especiales al árbol, tantos como sea necesario para que se cumpla la condición.
Nodos especiales: su objetivo es reemplazar las ramas vacías o nulas y no pueden tener descendientes.
La longitud de camino externo LCE es la suma de las longitudes de camino de todos los nodos especiales de un árbol.
en donde "h" = altura del árbol, "i" = nivel del árbol y "nei" = número de nodos especiales en el nivel "i".
La media de la longitud de camino externo:
Es el número de arcos que deben ser recorridos en promedio desde la raíz hasta un nodo especial cualquiera del árbol.en donde LCE = longitud de camino externo y "ne" = número de nodos especiales.
Árboles Binarios:
Es un árbol en el que ningún nodo puede tener más de dos subárboles. En este árbol cada nodo puede tener cero, uno o dos hijos; se conoce el nodo de la izquierda como hijo izquierdo y el nodo de la derecha como hijo derecho.Tipos de árboles binarios:
Distintos:
Dos árboles son distintos cuando sus estructuras son diferentes.Similares:
Dos árboles binarios son similares cuando sus estructuras son idéticas, pero la información que contienen es diferente entre sí.Equivalentes:
Son aquellos que son similares y además los nodos contienen la misma información.Completos:
Es un árbol en el que todos sus nodos, excepto los de último nivel, tienen dos hijos: el subárbol izquierdo y el subárbol derecho.Recorrido de un árbol binario:
Consiste en acceder una sola vez a todos sus nodos de una forma sistemática. Esta operación es básica en el tratamiento de árboles ya que nos permite imprimir o eliminar la información almacenada en un árbol.Hay tres métodos recursivos para hacer el recorrido de un árbol.
Preorden:
(raíz, izquierdo, derecho). Para recorrer un árbol binario no vacío en preorden, hay que realizar las siguientes operaciones recursivamente en cada nodo, comenzando con el nodo de raíz:
1. Visite la raíz
2. Atraviese el sub-árbol izquierdo
3. Atraviese el sub-árbol derecho
Inorden:
(izquierdo, raíz, derecho). Para recorrer un árbol binario no vacío en inorden (simétrico), hay que realizar las siguientes operaciones recursivamente en cada nodo:
1. Atraviese el sub-árbol izquierdo
2. Visite la raíz
3. Atraviese el sub-árbol derecho
Postorden:
(izquierdo, derecho, raíz). Para recorrer un árbol binario no vacío en postorden, hay que realizar las siguientes operaciones recursivamente en cada nodo:
1. Atraviese el sub-árbol izquierdo
2. Atraviese el sub-árbol derecho
3. Visite la raíz
Ejemplo:
Árbol binario de búsqueda:
- Secuencia de recorrido de preorden:
F, B, A, D, C, E, G, I, H (raíz, izquierda, derecha)
- Secuencia de recorrido de inorden:
A, B, C, D, E, F, G, H, I (izquierda, raíz, derecha); note cómo esto produce una secuencia ordenada
- Secuencia de recorrido de postorden:
A, C, E, D, B, H, I, G, F (izquierda, derecha, raíz)


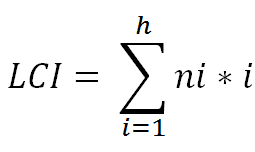












No comments